El teorema de Bernoulli, nos dice que al aumentar la velocidad
la presión disminuye, por lo tanto en las zonas donde la
presión ha disminuido aparecerán unas fuerzas
iguales en modulo, pero con sentido opuestos:
F = F´
Por lo tanto la esfera no experimentara ningún
desvío en su trayectoria.
Consideremos el caso de que la esfera gira, sobre el eje
perpendicular al dibujo:

Este giro, hace que arrastre una parte del fluido que hay a su
alrededor. Así, la velocidad en el punto 3 de la figura
será mayor que la existente en el punto 2.
V3 > V2
Por lo tanto al aplicar el teorema de Bernoulli las fuerzas
debidas a la presión no son iguales:
F > F´
Por lo tanto aparece una fuerza
aerodinámica neta, que tiende a desplazar la esfera en la
dirección F. Esto se conoce con el nombre
de efecto Magnus.
El efecto Magnus es bien conocido en muchos juegos de
pelota, en los que se conoce con el nombre de "efecto".
Perfil aerodinámico

En la figura se representa el perfil del ala de un
avión, con un determinado ángulo de ataque, dentro
de una corriente de aire laminar.
Si aplicamos de una manera cualitativa la ecuación de
continuidad y el teorema de Bernoulli, se llega a las siguientes
conclusiones:
- La máxima deformación de las líneas de
corriente se produce en la zona superior del borde de ataque,
por lo tanto hay un aumento de velocidad del fluido,
consecuentemente, esto lleva implícito una
disminución de presión, muy marcada en el borde
de ataque, disminuyendo hacia el borde de fuga. - Justo por debajo del borde de ataque se aprecia una zona
que no hay líneas de corriente (4), la velocidad del
fluido en esta zona es nula, es la denominada zona de remanso.
Por el teorema de Bernoulli la presión aumentará
en el borde de ataque, encontrando una zona de
sobrepresión, disminuyendo conforme se entra en el
perfil hacia el borde de fuga. - Finalmente por debajo del perfil y cerca del borde de fuga,
se produce un pequeño aumento de la velocidad y por lo
tanto una pequeña depresión, que compensará en
parte, la producida en la misma zona por encima del
perfil.

El resultado de la distribución de presiones, a lo largo del
perfil, es una fuerza dirigida hacia arriba, la componente de
esta fuerza perpendicular a la velocidad del viento será
la sustentación (F) que se encontrará aplicada en
el llamado centro de presiones (Cp).
Como se puede intuir, si variamos el ángulo de ataque,
también variará la distribución de las
líneas de corriente y en consecuencia las velocidades y la
distribución de presiones a lo largo del perfil. Esto
implicará una nueva distribución de fuerzas y una
nueva resultante aplicada a un nuevo centro de presiones.
En pruebas en
túneles de viento se establecen gráficas en las que se representan la
variación de Cp respecto al ángulo de ataque a del
perfil alar.
Teoría De Zhukovsky Aplicada A Una Superficie Plana
Sea una superficie plana e infinita, sin espesor, sin peso y
rígida, de ancho a (cuerda) e infinitamente larga, dentro
de una corriente de aire laminar de velocidad V, con un
ángulo de ataque a muy pequeño.


Siendo
x: la distancia al borde de ataque
+: para la superficie superior
–: para la superficie inferior

X = 0 v = ¥ X = a v = V
Sobre la superficie: v > V
Bajo la superficie : v < V
- La velocidad del aire v justo sobre la superficie,
tendrá como expresión: - La resultante de las fuerzas aerodinámicas por
unidad de longitud aplicadas en el centro de presiones
Cp es perpendicular a la dirección del viento e
igual a:
![]()
: densidad del aire
Dicha fuerza se puede descomponer en Fy perpendicular a la
superficie y Fx paralela a la misma. Fy es la resultante de las
fuerzas debidas a la presión dinámica y Fx es una
fuerza de succión en dirección del borde de ataque,
debida a las altas velocidades de la corriente de aire que se
genera.

Aplicando los postulados citados al principio, con respecto a
la superficie plana y dentro de una corriente de aire laminar V,
un pequeño ángulo de ataque a , observamos que:
Velocidad en la cara superior: Vs > V
Velocidad de la cara inferior: Vi < V
Estas velocidades tenderán a V conforme se acerquen al
borde de fuga.

La situación real en el borde de ataque de la
superficie no será infinita, tal como predice la
fórmula de Zhukovsky, sino más bien a una velocidad
alta como consecuencia de la deformación producida por el
"grosor" de la superficie.
Aplicando la ecuación de continuidad y el teorema de
Bernoulli a la distribución de velocidades, veremos que
existe una depresión en la cara superior, muy fuerte en el
borde de ataque y una sobrepresión en la cara inferior.
Decreciendo estas al alejarse del borde de ataque.
A medida que aumenta el ángulo de ataque, la corriente
laminar se degrada y empiezan a aparecer turbulencias.
Éstas, hacen cambiar la distribución de las
presiones y por tanto se modifica el centro de presiones (Cp).
Además, como el aire tiene una cierta viscosidad,
empiezan a aparecer fuerzas de rozamiento en la superficie, son
las llamadas fuerzas de remoción, que aparecen cuando el
ángulo a es importante.
Para diferentes ángulos de ataque, existirá una
posición del centro de presiones (Cp) distinta. Por medio
de resultados experimentales en túneles de viento, se mide
dicha posición. (ver gráfica).

Como se puede apreciar en la gráfica y de acuerdo con
la formula de Zhukovsky, para ángulos de ataque
comprendidos entre 0º y 20º, la posición del
centro de presiones (Cp), no varía y se localiza a un
cuarto de la distancia o cuerda "a"
3. Balance De Fuerzas En Una
Cometa Plana Ideal
Cometa plana ideal. Terminología
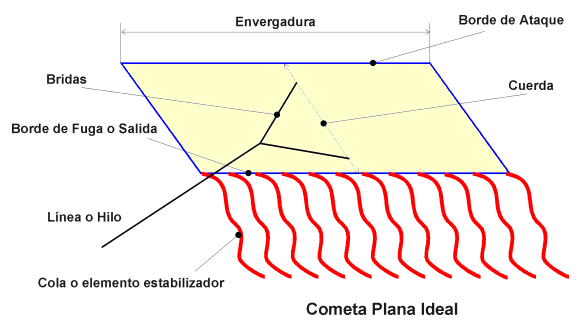
- Cometa ideal: Superficie plana, rígida, muy larga,
rectangular y mucho más ancha que alta. - Envergadura (e): Anchura máxima de la cometa.
- Cuerda (c): Dimensión de la sección central
de la cometa.  Aspecto
Aspecto
(D):- Brida: Dispositivo formado por uno o más cabos de
cuerda que sirven para unir la cometa con la línea o
hilo y permiten fijar el ángulo de ataque. - Hilo: Elemento de unión entre la cometa y el piloto.
En el caso de la cometa ideal tiene que ser resistente, ligero,
largo e inextensible. - Borde de Ataque: Borde de la cometa por donde incide el
viento. - Borde de Fuga o Salida: Borde de la cometa por donde sale
el viento. - Cola o elemento estabilizador: Como ocurre con cualquier
objeto volador, las cometas tienen tres ejes de
rotación: cabeceo, balanceo y guiñada. Para que
la cometa tenga un vuelo estable es necesario el control de
los tres ejes, impidiendo su giro respecto a los mismos.
Mediante el hilo y las bridas se consigue el control del
cabeceo y el balanceo. La guiñada se consigue mediante
una cola o elementos estabilizadores más complejos en
otros tipos de cometas.


 Velocidad
Velocidad
del viento ( ): Vector que define la velocidad y
dirección del viento respecto a tierra. Velocidad
Velocidad
de la cometa( ): Vector que define la velocidad y
dirección de la cometa respecto a tierra
 Velocidad Relativa ( )
Velocidad Relativa ( )
:Vector que define la velocidad y la dirección del
viento respecto a la cometa.- Ángulo de ataque (b ): Es el ángulo que
existe entre la cuerda y el vector de velocidad relativa. - Ángulo de incidencia (a ): Es el ángulo que
existe entre la cuerda y el vector de velocidad del viento. En
una cometa de un solo hilo b = a . - Elevación (q ): Es el ángulo que forma el
hilo y el suelo. - Centro de presiones (Cp): Punto de aplicación de la
resultante de todas las fuerzas aerodinámicas debidas al
viento. - Centro de gravedad (Cg): Punto de aplicación de
todas las fuerzas debidas a la gravedad o peso de la
cometa. - Centro de embridado (Ce): Punto de aplicación de la
fuerza de tensión del hilo.
Fuerzas Aerodinámicas En La Cometa Plana Ideal

Tal como se vio en el apartado donde se exponía
la teoría de Zhukovsky para una superficie plana, bajo un
determinado ángulo de ataque, el viento, al incidir sobre
la cometa, hace que aparezca una fuerza perpendicular a la
dirección del viento y aplicada en el centro de presiones
(Cp). Debido a que el aire no es un fluido ideal, el efecto de la
viscosidad, hace que exista una componente de resistencia en la
dirección del fluido, aplicada también en el centro
de presiones.
A la componente perpendicular a la corriente de aire (L), se
llama sustentación y a la paralela a la misma (D),
resistencia. La composición de ambas (Fa), es la
resultante de las fuerzas aerodinámicas.
La fuerza de sustentación, es la que tiende a elevar la
cometa, como veremos más adelante, venciendo el peso de la
cometa y del hilo. La fuerza de resistencia, que tiende a
arrastrarla, es compensada por la tensión del hilo.
Como ya se ha dicho anteriormente el valor estas
fuerzas aerodinámicas y la ubicación del centro de
presiones varían con el ángulo de ataque.
Fuerzas Gravitatorias En La Cometa Plana Ideal
Son el peso de la cometa y el peso del hilo.
En la cometa plana el peso (P) de la misma esta aplicado en el
centro de gravedad (Cg), el cual se ubica según sea la
geometría de la cometa.
El peso del hilo (PL) es la suma del peso propio del
mismo más su rozamiento con el viento. Estará
aplicado en el punto de unión de la brida con el hilo (B).
Esta circunstancia hace que se genere un momento que tienda a
variar el ángulo de ataque de la cometa
limitándonos la altura máxima a alcanzar por la
misma.
Las fuerzas de gravedad se oponen al vuelo de la cometa, esta
es la razón de que para poder volar
una cometa hay que emplear materiales
ligeros en su construcción.

Fuerzas Debidas A La Tensión Del Hilo En La Cometa
Ideal

Para que una cometa ideal vuele en equilibrio, la
fuerza de sustentación (L) debe vencer las fuerzas
gravitacionales (P y PL), pero esta fuerza
aerodinámica puede ser superior al peso y por tanto debe
aparece una tercera fuerza que compense este exceso, es la
denominada tensión del hilo (T).
La fuerza de tensión, se encuentra aplicada en el punto
de unión de la brida con el hilo (Cb), y es tangente en
ese punto a la forma que adquiere el hilo en el vuelo.
La tensión en ese punto se puede descomponer en una
componente vertical (Tv), que compensará el exceso de
fuerza de sustentación y una componente horizontal (Th),
que anulará el efecto de la resistencia del aire.
La tensión del hilo, se transmite a través del
mismo hasta el piloto, siendo la fuerza que hay que realizar para
mantener la cometa bajo control.
4. Equilibrio En El Vuelo De
Una Cometa Plana Ideal
"El equilibrio es tan solo un instante de perfección,
la estabilidad es más: es la permanente probabilidad
de que el equilibrio no esta lejos"
"Harm van Veen. The Tao of Kiteflying"
En este apartado, vamos a considerar las condiciones para que
una cometa plana ideal vuelo en equilibrio. Para simplificar las
cosas realizaremos este estudio sobre el plano vertical del
viento.

Un cuerpo sometido a un numero de fuerzas se dice que esta en
equilibrio cuando se cumple que la resultante de todas las
fuerzas es nula y el momento total respecto a cualquier eje de
giro esta compensado.
Una vez alcanzado el equilibrio hay que cerciorarse si el
mismo es estable. Esto ocurre si ante la respuesta a una
pequeña perturbación de su estado
(desplazamiento, empuje, etc.), el sistema se
desvía poco de esta posición de equilibrio,
reaccionando para volver a una posición estable. En caso
contrario el equilibrio será inestable.
Consideremos la cometa plana ideal con todas sus fuerzas
aplicadas:

1) Condiciones De Viento Fuerte
Para vientos superiores a 20 km./h, el peso P de la cometa
puede despreciarse en comparación con la fuerza
aerodinámica. Si aplicamos las condiciones de equilibrio
en esta nueva situación, se llega a la conclusión
que:

Conocido el centro de presiones de la cometa (Cp), ésta
estará en equilibrio si y solo si este coincide con el
centro de embridado. La fuerza aerodinámica Fa y la
tensión T tendrán el mismo modulo y sentidos
contrarios, perpendiculares a la superficie de la cometa. Al
coincidir Cp con Ce, no existirá ningún momento de
dichas fuerzas aplicadas.
Como Cp varía su posición con el ángulo
de ataque y como ya se vio cuando se explicó la
teoría de Zhukovsky aplicada a una superficie plana, se
puede realizar una gráfica que relacione dicho
ángulo de ataque y la posición del centro de
presiones.
Para c = 100 cm

Tenemos la siguiente gráfica:

Ejemplo: Si conocemos la posición del centro de
presiones, que se encuentra a 35 cm del borde de ataque, por
medio de la gráfica calculamos que el ángulo a =
27º.
La elevación de la cometa será: q = 90º – a
= 90º – 27º = 63º.
Para ángulos de ataque menores de 20º y posiciones
del centro de presiones por debajo de 25 cm, la cometa no
volará. A esta posición del centro de presiones lo
llamaremos centro de presiones crítico
(Cpcrítico).
Estabilidad
Dada una cometa en equilibrio, vamos ha estudiar
cualitativamente como se comporta la misma, ante una
perturbación de su posición de equilibrio.
Si partimos de la cometa en su posición de equilibrio,
y le aplicamos una perturbación (D ) en el borde de salida
,se producirá la siguiente situación:

La perturbación D aleja a la cometa de su
situación de equilibrio, el centro de presiones y el
centro de embridado se separan. Las fuerzas dejan de estar
alineadas, apareciendo un momento respecto a Cb, que en la
situación anterior era nulo. Este momento hará que
la cometa tienda a girar hasta alcanzar de nuevo la
posición de equilibrio.
Si la perturbación se produce en el borde de ataque de
la cometa:

El comportamiento
es similar, pero hay que tener en cuenta una nueva
condición, que el desplazamiento del nuevo centro de
presiones, no debe superar el punto crítico. Si la
perturbación es suficientemente importante para que se
alcance este Cpcrítico, se rompería el
equilibrio y la cometa entraría en perdida.
Hay que tener en cuenta también la disminución
del ángulo de ataque, que implica esta
perturbación, esto trae consigo una disminución de
la fuerza de sustentación, agravando más la
situación de equilibrio.
2) Condiciones De Viento Moderado O Débil
En el caso de existir un viento moderado, ya no se puede
despreciar la fuerza de gravedad, y por tanto la cometa presenta
este diagrama de
fuerzas:

La evaluación
del ángulo de ataque en la situación de equilibrio
se complica, ya que Cp y Cb, no coincidirá en el
equilibrio.
A pesar de todo, de una manera cualitativa podemos prever el
comportamiento posible de la cometa. Para lo cual nos
plantearemos dos situaciones posibles:
Centro de gravedad detrás
Sea una cometa con la siguiente distribución de fuerzas
y posición de los centros de presión, gravedad y
embridado. Esta distribución es la común en las
cometas planas con geometrías habituales.

Al ser el viento moderado, lleva consigo una
disminución de la fuerza aerodinámica (Fa) y por
tanto también la tensión (T), esto obliga a que la
cometa vuele con un gran ángulo de ataque,
desplazándose el centro de presiones hacia el centro de
gravedad, para intentar alcanzar el equilibrio.
Esta situación implica que la cometa perderá
altura y si la fuerza aerodinámica no compensa la
tensión y el peso, la cometa acabará aterrizando.
Ésta no es adecuada para volar con el viento
existente.
Centro de gravedad delante
Esta situación es la que nos encontramos en las cometas
tridimensionales.

La disminución del viento, hace como en el caso
anterior que disminuyan la fuerza aerodinámica (Fa) y por
tanto también la tensión (T).
Para que se pueda restablecer el equilibrio, el centro de
presiones tiene que desplazarse hasta el centro de gravedad. Esto
implica una disminución del ángulo de ataque,
acercándose al centro de presión crítico,
produciendo la entrada en perdida.
Esta es una de las razones de porque estas cometas no son
adecuadas para volar con vientos débiles.
Para que una cometa vuele con un viento débil, la
influencia del peso, se compensa aumentando el ángulo de
ataque de la cometa.
En estas condiciones, las geometrías que ante
superficies iguales, provoquen una mayor deformación de
las líneas de corriente en la dirección del viento,
serán las más adecuadas para volar con vientos
débiles. La relación de aspecto, nos
valorará esta circunstancia, así que, las cometas
que posean una D < 2, serán las más adecuadas
para volar con este tipo de vientos.

Estabilidad
La dinámica del equilibrio, para el caso de las cometas
que vuelan con vientos suaves es similar a lo expuesto para
vientos fuertes, con la peculiaridad de que el peso tendrá
una influencia en el ángulo de ataque inicial.
5. Efectos de la deformación axial y diedrica en el
vuelo de una cometa ideal
Cuando vuela una cometa, sobre su superficie aparecen una
serie de deformaciones consecuencia de la fuerza del
viento.

Consideremos dos tipos de deformaciones: la axial (cambio de
curvatura en el sentido de la cuerda de la cometa) y la
diédrica (ángulo que se forma a lo largo de la
envergadura de la cometa respecto al plano, que se apoya en la
espina central).
Dependiendo de la forma de la cometa y de la
disposición de las bridas, la deformación axial
puede ser cóncava o convexa.

Influencia De Las Deformaciones En Las Gráficas (a – x/c)

Deformación Axial
Como ya se vio en el apartado del estudio del equilibrio,
una cometa plana no puede presentar una ángulo de ataque
inferior al crítico, lo que es lo mismo, que el centro de
embridado nunca supere la posición del centro de presiones
crítico. Una cometa en estas condiciones entrará en
pérdida y caerá al suelo.

Si la cometa se vuelve convexa, la gráfica nos muestra que a
toda posición de Cp le corresponde un ángulo
determinado. El centro de presiones crítico se
sitúa muy cerca del borde de ataque. Como la curva siempre
es creciente (a – x/c), la cometa siempre conserva su
estabilidad. Ante cambios de la velocidad del
viento, una convexidad moderada es beneficiosa, ya que permite
que el ajuste no sea crítico.

Si la cometa se vuelve cóncava, por debajo de un
ángulo crítico la gráfica es decreciente, lo
que implica que si aumenta el ángulo de ataque desde cero
hasta el ángulo crítico, la posición del
centro de presiones se irá acercando al borde de ataque,
con la consiguiente tendencia a planear hacia la posición
del piloto. La cuerda o hilo se quedará sin tensión
y entrará en pérdida.
Podemos diseñar la cometa cóncava dentro de la
zona de planeo, siempre que las bridas de la cometa, se ajusten a
un determinado centro de embridado, para las diferentes
velocidades del viento.
Por encima del ángulo critico, la cometa debe tener un
comportamiento
estable.
Consideremos el caso de que una cometa plana, en su
posición de equilibrio, se vuelve cóncava o
convexa.
Si mantenemos el mismo centro de embridado, que en la
posición de equilibrio, para viento fuerte, coincide con
el centro de presiones, según se ha visto anteriormente,
un aumento de la convexidad obliga a la cometa aumentar el
ángulo de ataque para restablecer el equilibrio,
según se ve en la gráfica. Como consecuencia de
ello disminuirá el ángulo de elevación (q =
90º – a ), y la cometa perderá altura.

Por el contrario, un aumento de la concavidad, para
ángulos de ataque superior al crítico (fuera de la
zona de planeo), obliga a la cometa a disminuir el ángulo
de ataque para restablecer el equilibrio, según se ve en
la gráfica. En este caso, aumentará el
ángulo de elevación y la cometa ganará
altura


Deformación Diédrica
En una cometa con una sola brida central, la fuerza del viento
tiende a plegar la estructura
hacia atrás y por tanto aumenta el ángulo
diédrico.
Para entender los efectos de este tipo de alteración
estructural, utilizando los resultados experimentales obtenidos
en los túneles de viento, son los que se reflejan en la
gráfica.
Se observa que un aumento en el ángulo diédrico
no implica una variación de la forma de la curva. Luego la
reacción de la cometa frente una perturbación
externa no se ve afectada, es decir, conserva las mismas
características en cuanto a su estabilidad.
Respecto al ángulo de ataque, si se mantiene el centro
de embridado, al aumentar el ángulo diédrico la
cometa aumenta su ángulo de ataque. Este aumento, se
traducirá nuevamente en una disminución de la
altura de vuelo, tal como ocurría con la convexidad.
6. El centro de embridado en
la cometa plana ideal
En la mayoría de las cometas, el hilo no se ata
directamente a la estructura de la misma, sino que se hace a la
denominada brida.
La brida, posee con independencia
de su forma y geometría, las siguientes misiones
básicas:
- Fijan el ángulo de ataque de la cometa
- Repartir la tensión del hilo entre los distintos
puntos de la estructura de la cometa. - Permite el control del
cabeceo y del balanceo.
Brida Básica
Imaginemos un triángulo formado pos tres varillas,
rígidas, de material muy ligero y articulada en los
extremos. Aplicaremos un peso P, en la vertical del punto de
sustentación.

En esta estructura aparecerán las siguientes
fuerzas:
![]()

Si el peso P, es mucho más grande que el peso de las
armaduras, el conjunto se mantendrá en equilibrio. Las
varillas "a" y "b", están trabajando a tracción y
la "c" a compresión. Por tanto, se puede sustituir las
varillas "a" y "b" por hilos resistentes.

Consideremos una cometa ideal en equilibrio con viento fuerte,
que según se vio, el centro de embridado coincide con el
centro de presiones (Cp = Ce).
Para la brida considerada supongamos que hacemos x/c = 0,25,
es decir. que Cp se encuentra a c/4 del borde de
ataque.
Representaremos ra, rb y rc normalizadas
a la tensión T en función de
y/c.

Para y/c = 0,3 " rb / T = 1 ra / T = 0,7
rc / T = 0,65
Esto quiere decir, que la tensión en el hilo es igual a
la de la brida "b", el 70% en "a" y el 65% en "c".
Por ejemplo, si la tensión en el hilo T = 15 Kg,
tendremos:
ra = 15 x 0,7 = 10,5 Kg
rb = 15 Kg
rc = 15 x 0,65 = 9,8 Kg
Si observamos la gráfica, para relaciones y/c < 0,3,
los esfuerzos que se generan en las armaduras aumenta
considerablemente:
Para y/c = 0,1 " rb / T = ra / T = rc / T
= 2
Lo que resulta que para T = 15 Kg, tendremos:
ra = rb = rc = 2 x 15 = 30
Kg
Estos valores
podrían romper los hilos de las bridas y plegar la
estructura de la cometa.
Por otro lado, para valores de y/c > 1, los esfuerzos en
los hilos y en la estructura de la cometa no varían
mucho.
Por tanto como conclusión:
" La relación y/c en una brida, tendrá un
valor
comprendido entre 0,3 y 1 "
0,3 < y/c < 1
Si por algún motivo, es necesario utilizar una brida
con la relación y/c inferior al valor 0,3, tendremos que
usar un fijador central o una quilla.

Consideremos las dos situaciones siguientes:

Estos casos son las llamadas "falsas bridas". Si observamos el
caso 1, las fuerzas T y Fa tienden a separar los puntos Ce y Cp.
Para impedir la deformación de la armadura "a b c", el
segmento "a" tiene que ser una varilla rígida, ya que
trabaja a compresión.
La situación límite de la falsa brida es la
correspondiente al caso 2. Aquí se puede observar que el
segmento "b", está en línea con las fuerzas T y Fa.
Esto significa que el ángulo de ataque queda fijado por el
Cp escogido, y el segmento "a" no hace ningún tipo de
esfuerzo, pudiendo ser eliminado.
Por regla general, la falsa brida da malos resultados, por
tanto:
" La brida ha de estar unida a la estructura de la cometa, de
manera que Cp este situado dentro del segmento c "
Estos criterios utilizados para bridas triangulares, pueden
ser empleados en bridas tridimensionales (tetraédricas,
etc.).
Como resumen podemos decir que para escoger el centro de
embridado más correcto se deben cumplir las tras
reglas:

Efecto De La Separación Entre Los Puntos De
Unión De Las Bridas
Consideremos las siguientes uniones de una brida simple:

Uniones cerca del centro de presiones
Los casos 1, 4, y 7 tienen en común, que en todos
ellos, los puntos de atado de la brida a la estructura se
encuentran cerca del centro de presiones (Cp).

En estas condiciones, la fuerza del viento tenderá a
deformar la cometa, dándole cierta convexidad, esto se
traducirá inevitablemente en un aumento del ángulo
de ataque y en una pérdida de la altura de vuelo.
Por lo que respecta a la estabilidad longitudinal, el ajuste
es un poco más crítico, que cuando las uniones
están más separadas. Esta dificultad aumenta a
medida que la relación y/c crece, como en los casos 4 y
7.
Uniones cerca de los extremos
Son las uniones más utilizadas, ya que dan los mejores
resultados.
Este tipo de unión (casos 3, 6 y 9), hace que la cometa
se estabilice longitudinalmente y permite un ajuste más
preciso del centro de presiones.
La estructura de la cometa tiene que ser rígida, para
evitar un efecto que aparece a cierta velocidad del viento: el
"galopeo".
Este efecto, tiene su explicación por la concavidad que
aparece en la estructura. Esto hace que la cometa gane altura y
disminuya por lo tanto su ángulo de ataque, lo que implica
una disminución de la fuerza aerodinámica. La
estructura recuperará la forma plana.

Pero como ha disminuido la fuerza aerodinámica, la
cometa pierde la altura que había ganado, aflojando la
tensión del hilo. Seguidamente, la cometa se
desplazará hacia atrás, hasta que la línea
vuelva a tener suficiente tensión y se vuelva a repetir el
ciclo, indefinidamente.
Uniones compensadas

Las bridas se unen a la armadura, en puntos intermedios que
compensen los efectos anteriores. Estas uniones son las
más empleadas en las cometas deportivas o de dos
hilos.
Modificando las posiciones de los puntos de unión, es
posible llegar a una disposición tal, que el efecto de
pérdida de altura por la convexidad de los extremos, quede
compensada por el aumento de altura que propicia la concavidad
entre las uniones.
Efecto De La Longitud De Las Bridas
En condiciones de viento fuerte y sin tener en cuenta el
efecto de la deformación de la estructura, cuanto
más grande es la relación y/c, más estable
es la cometa.
Sean dos cometas, con diferente relación y/c en sus
bridas, y las perturbamos por el borde de fuga.

Si la misma perturbación (D ), afecta a las dos
cometas, la separación de los puntos Ce´ y Cp´
será mayor en el caso 2. Por tanto, la magnitud del
momento reparador M2 será más enérgico que
M1. Esto hará que la cometa 2 recupere el equilibrio
más rápido que la 1, en otras palabras, la cometa 2
admite perturbaciones más fuertes.
Además con la relación y/c con un valor
próximo a 1, se reducen las tensiones de las cuerdas de
las bridas y el esfuerzo de la estructura (deformaciones).
Por otro lado, con vientos suaves, las bridas largas tienen
tendencia a corvarse y perder su condición de
indeformabilidad. Eso provoca una cierta inestabilidad, en forma
de cabeceo, pero sin pérdida de control.
Por lo tanto, como nunca evitaremos las deformaciones, podemos
dar la cuarta regla para la situación del centro de
embridado:
"Las uniones de las bridas a la armadura de la cometa, se han
de situar de manera que compensen el efecto de las
deformaciones".
7. Principios De
Semejanza En Una Cometa Ideal
Vamos a estudiar en este apartado, que efectos ocurren en una
cometa ideal si construimos otra cometa semejante, aumentando o
disminuyendo sus dimensiones.
Cuando variamos las dimensiones de una cometa, para que su
vuelo lo haga en las mismas condiciones, no basta que su forma
sea semejante, es necesario que se cumplan unas relaciones
sencillas para conseguir la semejanza física.
Supongamos que duplicamos la escala de una
cometa, su superficie aumentará cuatro veces, pero en
cambio su volumen lo
hará ocho.
La fuerza aerodinámica en un cometa es proporcional al
área efectiva y a la velocidad del viento al cuadrado:
Fa ~ A vv2
El peso (P) depende de la densidad o peso
especifico (r ) de los materiales que
esta formada la cometa, así éste será
proporcional al volumen (V) de la misma:
P ~ r V
Por lo tanto, si aumentamos la escala de la cometa dos
veces, la fuerza aerodinámica aumentará en la misma
proporción que la superficie (cuatro veces), pero el peso
lo ha hecho en la misma proporción que el volumen (ocho
veces). Luego la cometa escalada no volará, al menos que
aumente la velocidad del viento o la hagamos más
ligera.
Con esto se quiere decir, que es necesario mantener unas
condiciones para que el aumento o disminución en la escala
de una cometa no afecten a las características del
vuelo.
Formulas de semejanza

Sea L una dimensión lineal de la cometa, su superficie
será:
A = L2
Con la cometa en equilibrio, la fuerza aerodinámica es
igual al peso;
Fa = P
Como:
Fa ~ A vv2
P ~ r V ~ r L3
Implica:
P ~ A vv2
![]()
Definamos una relación denominada "ratio de masa" (MR),
que relaciona la masa de aire desplazada
por la cometa con la masa de la misma. Este número
adimensional, se puede estimar como:
Masa de aire desplazada ~ L3
Masa de la cometa ~ P
![]() Luego:
Luego:
Condiciones para los cambios de escala
L1 = X L
A1 = X2 A

Conclusión, el peso debe aumentar en el factor de
escala al cuadrado
Conclusión, se debe aumentar el ratio de masa en el
mismo factor de escala.- Sea una cometa con dimensiones L, volando con una velocidad
del viento Vv. Realicemos un cambio de escala de factor X,
¿Cuál debe ser el nuevo peso (P1) y el nuevo
ratio de masa (MR1), para que la cometa vuele con el mismo
viento?. - Sea la cometa de dimensiones lineales L, realicemos un
cambio de escala de factor X, manteniendo el mismo ratio de
escala. ¿Cuál debe ser el nuevo peso (P1) y con
qué nueva velocidad del viento volará?.
L1 = X L
A1 = X2 A
MR1 = MR


Luego el peso debe aumentar en el factor de escala al
cubo.
Luego la velocidad del viento nueva con la que volará
la cometa es:
![]()
Tabla Resumen
CONDICIÓN 1 | CONDICIÓN 2 | ||
VELOCIDAD DEL VIENTO INVARIABLE | RATIO DE MASA INVARIABLE | ||
X>1 | X<1 | X>1 | X<1 |
No varía la carga vélica | No varía la carga vélica | Mayor carga vélica (P/A) | Menor carga vélica (P/A) |
El peso crece con el área | El peso disminuye con el área | El peso crece con el volumen | El peso disminuye con el volumen |
Mayor estabilidad | Menor estabilidad | En vientos fuertes alguna perdida de | La estabilidad no cambia o a veces crece |
Se necesita un material más | Se puede utilizar un material más | Se necesita más viento para | Se necesita menos viento para volar |
Trabajo recopilado y enviado por:
Juan Miguel Suay Belenguer
 Página anterior Página anterior |   Volver al principio del trabajo Volver al principio del trabajo | Página siguiente  |



